


Next: Combining Probabilities
Up: Basic Ideas
Previous: Basic Ideas
The simplest form of probability functions are discrete probabilities.
In this case, we have some variable 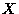 which can take different
values or outcomes,
which can take different
values or outcomes, 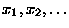 .
.
- Examples:
- if
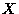 represents a statement such
as ``it will rain tomorrow'', it can take two values TRUE and FALSE;
if
represents a statement such
as ``it will rain tomorrow'', it can take two values TRUE and FALSE;
if 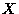 represents the result of a coin flip,
there would be the two possible outcomes,
represents the result of a coin flip,
there would be the two possible outcomes, 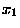 meaning heads and
meaning heads and
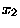 meaning tails; if
meaning tails; if 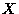 is the number drawn in the next lottery
draw, there would be 13,983,816 possibilities.
is the number drawn in the next lottery
draw, there would be 13,983,816 possibilities.
We denote the probability that 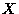 takes a
particular value
takes a
particular value 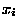 as
as 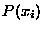 . The probability must be between
. The probability must be between
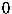 and
and 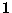 . If
. If 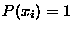 ,
, 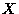 takes the value
takes the value 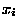 with
certainty; if
with
certainty; if 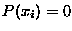 ,
, 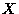 definitely does not take the value
definitely does not take the value 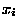 ;
the closer is
;
the closer is 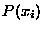 to
to 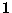 , the greater the likelihood that
, the greater the likelihood that 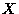 takes this value.
Assuming that
takes this value.
Assuming that 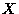 can take only one of the values at a time (the
values are mutually exclusive), the probability that
can take only one of the values at a time (the
values are mutually exclusive), the probability that 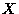 takes
takes 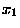 or
or 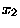 is
is 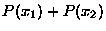 . Since
. Since 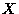 must take some value, the sum
of the the probabilities of all possibly values is
must take some value, the sum
of the the probabilities of all possibly values is 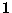 . Thus, the
probability is normalised,
. Thus, the
probability is normalised,
which means that 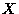 always takes one of its allowed values.
always takes one of its allowed values.
We are often interested, however, in cases in which a random variable
takes a continuous range of values. In this case, the above must be
modified. We write a probability distribution or density 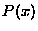 as a function of
the continuous variable
as a function of
the continuous variable 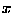 .
.
- Example:
- A farmer might be
interested in the probability that a given amount of rainfall will
occur in a particular growing season. The rainfall,
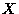 , could be
modelled by a continuous positive real number
, could be
modelled by a continuous positive real number 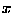 .
.
We cannot interpret 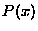 as the
probability that
as the
probability that 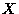 takes the value
takes the value 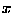 , because that probability is
almost always going to be
, because that probability is
almost always going to be 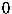 . You cannot have an infinite number of
possibilities with nonzero probability, because it could not be
normalised. For continuous distributions,
. You cannot have an infinite number of
possibilities with nonzero probability, because it could not be
normalised. For continuous distributions, 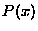 is defined so that
the probability that
is defined so that
the probability that
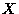 is between
is between 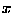 and
and 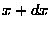 is
is
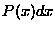 , where
, where 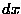 is arbitrarily small.
The normalisation condition converts from a sum to an integral, and
is,
is arbitrarily small.
The normalisation condition converts from a sum to an integral, and
is,



Next: Combining Probabilities
Up: Basic Ideas
Previous: Basic Ideas
Jon Shapiro
1999-09-23
![]() which can take different
values or outcomes,
which can take different
values or outcomes, ![]() .
.
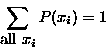
![]() as a function of
the continuous variable
as a function of
the continuous variable ![]() .
.