Conditional Probabilities are of Fundamental Importance

The conditional probability is an essential quantity in wide range of domains, including classification, decision theory, prediction, diagnostics, and other similar situations. That is because one typically makes the classification, decision, prediction, etc. based on some evidence. Thus, what one wants to know is the probability of the result given the evidence 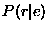$P(r\vert e)$. In the example of classification, the evidence is the values of the measurements, or the features on which the classification is to be based. The possible results are the possible classes. The problem is that this conditional probability is very difficult to estimate from experiments directly. This is because there are typically a huge number of values which the features can take. Thus there would be an enormous number of conditional probabilities to estimate. To get around this, Bayes rule is used to write this in terms of the conditional probability of getting the evidence given the classification. The probability of the evidence conditioned on the result can sometimes be determined from first principles, and is often much easier to estimate. There are often only a handful of possible classes or results. For a given classification, one tries to measure the probability of getting different evidence or patterns. A model is used to interpolate to unseen patterns. This gives an estimate of the conditional probability of the evidence given the classification. Using Bayes rule, we use this to get what is desired, the conditional probability of the classification given the evidence.