An example may illustrate the difference between the joint probability
and the conditional probability. Suppose we pick an arbitrary British
adult. We wonder about two things: is this person rich and did they
attend public school? Thus, we have two variables:
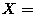 the person is rich,
the person is rich,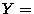 the person went to public school.
the person went to public school.
The variables 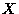 and
and 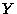 can each take two values, TRUE and
FALSE. Presumably, the probability that the person is rich is small, as is
the probability that they attended public school, because there are 10s of
millions of British adults, few of them are rich, and few of them
attended public school. The joint probability, the probability that the person
is both rich and an alumnus of public school is smaller still, since that is the
fraction of British adults who are both rich and public school grads.
can each take two values, TRUE and
FALSE. Presumably, the probability that the person is rich is small, as is
the probability that they attended public school, because there are 10s of
millions of British adults, few of them are rich, and few of them
attended public school. The joint probability, the probability that the person
is both rich and an alumnus of public school is smaller still, since that is the
fraction of British adults who are both rich and public school grads.
Now, consider the conditional probability,
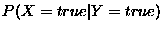 . That is
the probability that a British adult is rich given the fact that
they went to public school, i.e. the fraction of public school alumni who are rich. I
would assume that this is closer to 1, adults who went to public school are
likely to be rich (I assume this is true).
. That is
the probability that a British adult is rich given the fact that
they went to public school, i.e. the fraction of public school alumni who are rich. I
would assume that this is closer to 1, adults who went to public school are
likely to be rich (I assume this is true).
![]() and
and ![]() , we might want combined
probabilities involving both
, we might want combined
probabilities involving both ![]() and
and ![]() . There are three ways of
combining random variables.
. There are three ways of
combining random variables.
![]() . That is
the probability that a British adult is rich given the fact that
they went to public school, i.e. the fraction of public school alumni who are rich. I
would assume that this is closer to 1, adults who went to public school are
likely to be rich (I assume this is true).
. That is
the probability that a British adult is rich given the fact that
they went to public school, i.e. the fraction of public school alumni who are rich. I
would assume that this is closer to 1, adults who went to public school are
likely to be rich (I assume this is true).