


Next: B. The Gaussian or
Up: Appendices Important
Previous: Appendices Important
This you have seen in CS1021. It is also called a Bernoulli
distribution. It is applicable to the situation where there are 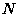 independent trials, each of which can have one of two outcomes. Call
one of the outcomes
independent trials, each of which can have one of two outcomes. Call
one of the outcomes 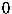 and the other
and the other 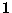 . Let
. Let 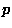 be the probability
that any trial yields the outcome
be the probability
that any trial yields the outcome 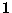 . Then the probability of getting
. Then the probability of getting
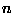 1's in
1's in 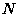 trials is given by
trials is given by
where
The expected mean number of 1's is 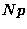 ; the variance is
; the variance is 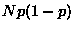
In the limit of large 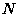 with
with 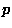 fixed, a binomial distribution is
well approximated by a continuous Gaussian distribution, with the
appropriate mean and variance.
fixed, a binomial distribution is
well approximated by a continuous Gaussian distribution, with the
appropriate mean and variance.
Jon Shapiro
1999-09-23
![]() with
with ![]() fixed, a binomial distribution is
well approximated by a continuous Gaussian distribution, with the
appropriate mean and variance.
fixed, a binomial distribution is
well approximated by a continuous Gaussian distribution, with the
appropriate mean and variance.