Estimating Probabilities from Data -- Statistics

In probability textbooks, you are often given examples in which the underlying probability model is known, and you have to give the likelihood of some data. For example, you might be asked to calculate the probability of flipping 18 heads in a row. It is known (or assumed) that the probability of a coin coming up heads is 1/2, and it is a simple application of the rules for combining probabilities. (Specifically, each flip is independent so the probabilities multiply to give 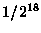$1/2^{18}$.)

However, often one is faced with the inverse situation -- there is some data from which you would like to infer the underlying probability model. This is the problem tackled by ``statistics''.

Examples:

Estimate the probability of getting CJD from eating beef as a distribution function of the amount of beef consumed from a sample of beef eaters; estimate the probability of a computer program performing correctly from test runs.

The problem of the estimation of discrete probabilities is easiest and is dealt with first. The problem of estimation of a probability distribution of continuous variables is important in Bayesian classification, but only the most elementary methods are given here.