This chapter investigates the SCALP architecture and implementation to see how well it meets its stated objective high power efficiency through high code density, parallelism and asynchronous implementation. The first sections introduce tools and example programs that have been used to carry out the evaluation. Subsequent sections describe the results of the evaluation.
The gate level VHDL model was evaluated as follows: a number of forms of test stimulus were developed to exercise the model in interesting or representative ways. The model was then extended by the addition of instrumentation code that reports internal activity during execution of the stimulus. The activity trace thus obtained was subsequently analysed by a number of evaluation programs to report statistics about the behaviour of the processor.
The test stimuli used take the form of example programs and instruction sequences.
Six instruction sequences have been written with different properties as described below. The sequences each execute approximately 1000 instructions. They are not "real programs" in the sense that they do not carry out any useful work.
(i) Distributed independent instructions (dis-ind)
An instruction sequence comprising instructions well distributed between the functional units with the minimum of data dependencies. There are no taken branches.
(ii) Non-distributed independent instructions (ndis-ind)
An instruction sequence comprising instructions that concentrate on one functional unit for some time making it a bottleneck before moving to the next. Few data dependencies exist between the instructions. There are no taken branches.
(iii) Distributed dependent instructions (dis-dep)
An instruction sequence comprising instructions well distributed among the functional units with many data dependencies. There are no taken branches.
(iv) Non-distributed dependent instructions (ndis-dep)
An instruction sequence comprising instructions that concentrate on one functional unit for some time making it a bottleneck before moving to the next. There are many data dependencies between the instructions. There are no taken branches.
(v) Independent branches (ind-br)
An instruction sequence comprising instructions well distributed among the functional units with few data dependencies. One instruction in five is an unconditionally taken branch.
(vi) Dependent branches (dep-br)
An instruction sequence comprising instructions well distributed among the functional units with many data dependencies. One instruction in five is a taken branch which is dependent on the preceding instructions.
The lack of a high level language compiler for SCALP makes evaluation with real programs difficult. Five simple example programs have been written in SCALP assembly language. Brief descriptions of the programs follow.
(i) Shading
A short piece of code that implements the inner loop of the Gouraud shading algorithm: a number of sequential memory locations are loaded with values that differ by a constant amount.
(ii) Word Count
A loop whose function resembles the unix "wc" program: the number of words and lines in an area of memory are counted.
(iii) String Tree Search
A binary tree with string key values is searched recursively for values that may or may not be present.
(iv) Quicksort
The O(n log n) recursive sorting algorithm is applied to an array of integers.
(v) Sumlist
Integer values in a null-terminated linked list are summed.
For comparison the same programs have also been written in assembly language for two conventional processors, ARM and "ARMLESS". ARMLESS is a hypothetical processor whose instruction set is a subset of the ARM similar to the SPARC processor. Its properties are
All instructions are 32 bits long.
14 general purpose registers.
Instructions specify three registers or two registers and an immediate for sources and destinations.
Only load and store instructions access memory.
Branch instructions may be conditional on the value of the condition codes.
The ARM instruction set [FURB89] also features:
All instructions may be conditional on the value of the condition codes.
Load and store instructions may write incremented base register values back to the register bank.
Load and store multiple instructions may transfer any group of registers to or from memory in a single instruction.
Load and load multiple instructions may transfer the program counter to effect a branch.
A number of programs have been written to analyse the output of the instrumented VHDL model.
Being able to see graphically the flow of data within a processor can be a great help to understanding limits on performance such as bottlenecks and dependencies. This is especially true in asynchronous systems where time domain behaviour is less constrained than in a synchronous design.
Other work has applied visualisation to asynchronous pipelines executing SPARC code [CHIE95] and to the AMULET processor [SWAI95].
A visualisation program, xpipevis, has been developed to show SCALP's internal data flow graphically. Using this tool it is possible to see where bottlenecks occur and what the processor's typical behaviour is. The program displays a block diagram of the processor on which each bus is illuminated using a colour corresponding to its state: idle, busy, or reseting. The visualisation can run either at a constant rate relative to the simulated real time or in "single step" mode where the user presses a key to advance the display. A snapshot of the typical output from the program is shown in figure 7.1.

xpipevis has proved useful for optimising the SCALP implementation, for example when choosing the number of stages in the instruction and operand queues and the configuration of the result network.
A common objective in parallel system design is to obtain a high utilisation of the available resources. If some resources are rarely or never being used the design may be optimised by removing them; on the other hand if a particular resource is often fully used it may limit the performance of the system as a whole.
A program has been written to measure the utilisation of the functional units, the result network busses and the queue stages in the instruction fifo, functional unit instruction and operand queues, and the functional unit result queues.
A simple program has been written to measure the processor's instruction execution rate in terms of instructions per second.
Where a set of benchmark programs is used to evaluate the performance of a processor it is useful to be able to compute a summary value indicating overall performance. If the benchmark programs constitute a representative workload for the processor then the arithmetic mean of the individual execution times can be used to predict the total execution time for the workload.
In some cases the benchmarks used are artificial or do not constitute a real workload. In this case no measure can indicate real performance but some sort of summary value is still useful. The arithmetic mean has the particular disadvantage that the benchmarks whose execution times are greatest will dominate the result. In contrast the geometric mean gives equal importance to all benchmarks.
Consider the data in table 7.1, which shows execution times for two programs A and B on two machines X and Y. X does twice as well as Y on A, but Y does twice as well as X on B, so in some sense they are equally good overall. This is indicated by their equal geometric means. The arithmetic mean on the other hand is biased by the fact that A takes less time than B on both machines.
Machine X Machine Y
Program A 10 20
Program B 100 50
Arithmetic Mean 55 35
Geometric Mean 31.6 31.6
[HENN90], pages 50-53, discusses the relative merits of the arithmetic and geometric means for this type of analysis.
In this section the code density achieved by SCALP is evaluated. High code density was an objective of the design because the reduced memory bandwidth resulting from high code density is beneficial to power efficiency.
Tables 7.2 and 7.3 present the static and dynamic code sizes measured for SCALP and the conventional processors ARM and "ARMLESS", using the example programs described in section 7.1.1.
Program SCALP ARM ARMLESS
Shading 37 44 48
Word Count 54 48 56
String Tree Search 126 116 136
Quicksort 189 168 200
Sumlist 27 32 36
Geometric Mean 66.3 66.7 76.6
Program SCALP ARM ARMLESS
Shading 1024 1024 1280
Word Count 3290 3128 3656
String Tree Search 382 420 500
Quicksort 13194 5908 6648
Sumlist 315 380 464
Geometric Mean 1398 1247 1485
In terms of static code density, SCALP does about as well as the ARM processor and about 13% better than "ARMLESS".
In terms of dynamic code density, SCALP does about 12% worse than ARM and about 6% better than "ARMLESS".
These results are worse than expected and result from a greater than expected overhead of register bank and move unit instructions. These instructions are required to move operands when the explicit forwarding mechanism is insufficient. Table 7.4 shows the number of register bank or move unit instructions required per "useful" instruction.
Benchmark Instructions
Shading 0.99
Word Count 0.72
String Tree Search 1.06
Quicksort 1.34
Sumlist 0.61
Geometric Mean 0.91
The large number of these instructions can be attributed to a flaw in the explicit forwarding mechanism that makes it less useful to the programmer than the results concerning the frequency of forwarding cited in table 2.3 might lead one to expect. The consequence is that many results are written to the register bank immediately after being computed and are read from there before each use.
This failing of the instruction set explained further in section 7.8.
This section investigates the throughput of SCALP's pipeline and the parallelism that it is able to achieve between stages. Firstly the cycle times of the individual pipeline stages are considered and then the processor as a whole is examined using the instruction sequences and example programs described in section 7.1.1.
Times in this section are generally expressed in terms of standard gate delays (GD). These can be related to real execution times if a particular technology is considered. Section 7.5 performs this comparison.
The FIG fetch stage comprises three components: the fetcher, the memory interface and the memory itself. In the test environment the fetched FIGs are fed to the FIG fifo, but the output of the fifo is "short circuited" so that its rate of consumption of FIGs is maximised. No load or store activity is present.
The cycle time of the FIG fetcher in the absence of branch instructions has been measured and is shown in table 7.5.
Cycle time / GD
117
The performance of the instruction issuer has been measured by connecting it between the FIG fifo and the functional unit instruction queues as normal but with the other ends of these queues short circuited to provide maximum performance. The performance is dependent on the instructions being issued; when the instructions are evenly distributed among the functional units the performance will be greater than when the instructions are clustered within a subset of the functional units. The cycle times for various representative FIGs are shown in table 7.6. All branch instructions are not taken.
The cycle time when deleting instructions skipped over after a taken branch has also been measured and is also shown.
Instructions Cycle time / GD
(A-E=functional units, I=immediate)
Chunk 0 Chunk 1 Chunk 2 Chunk 3 Chunk 4
A B C D I 54
A A B C D 66
A A A B C 93
A A A A B 124
A A A A A 155
Deleting skipped over instructions 75
These results are plotted in figure 7.2. It can be seen that when two or more instructions in a single FIG are for the same functional unit the issuer's cycle time is approximately 31 GD per instruction for that functional unit. This suggests that in this case the cycle time is limited by the issuer's output speed. When no functional unit receives more than one instruction from a single FIG the cycle time is 54 GD, presumably limited by the issuer's input speed.
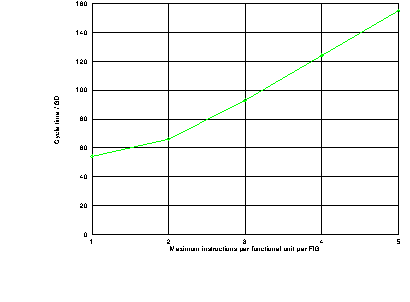
The performance of each functional unit has been measured by connecting it between instruction, operand, and result queues as normal but with the other ends of the queues short circuited to provide maximum performance. The load/store unit was connected to the memory via the memory interface but no instruction fetch activity was present to compete for the memory bandwidth. The branch unit's connection to the fetcher was also short circuited. The cycle times for each of the functional units for various representative instructions are shown in table 7.7. For those instructions which involve an addition or similar operation the cycle times were measured for a number of different operands which cause different carry propagation lengths.
Functional Instruction Carry Cycle time / GD
Unit Length
ALU Logical function - 38
Logical comparison - 41
Arithmetic function 0 47
4 52
10 65
32 107
Arithmetic comparison 0 49
4 54
10 67
32 109
Move Duplicate, Sequence - 70
Conditional Move, Move Link - 44
Register Bank Read - 42
Write - 35
Load / Store Load 0 79
32 123
Store 0 72
32 116
Branch Non-taken conditional - 26
Taken conditional
or unconditional 0 69
4 69
10 70
28 110
Computed branch - 48
Branch and link 0 77
The performance of the result network has been measured by connecting it between the functional unit result queues and the operand queues as normal but with the ends of these queues short circuited to maximise performance. The result is given in table 7.8.
Cycle Time / GD
47
The performance of each of the isolated stages in the absence of taken branches is summarised in table 7.9. This data is also shown in figure 7.3.
Stage Cycle Time / GD
Instruction fetch (no branches) per FIG 117
Instruction issuer (input side) per FIG 54
Instruction issuer (output side) per instruction,
each output 31
ALU (representative arithmetic operation) 54
Move unit (two cycle instruction) 70
Register read 42
Register write 35
Load (representative operation) 84
Store (representative operation) 77
Untaken branch 26
Result network 47
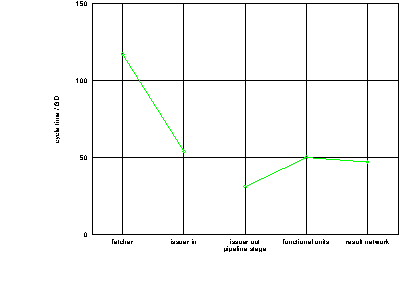
In the first part of the pipeline which deals with FIGs the throughput is limited by the cycle time of the instruction fetcher of 117 GD.
In the second part of the pipeline which deals with individual instructions throughput is generally limited by the functional units. The issuer output generally does not limit performance because its cycle time of 31 GD is less than nearly all functional unit cycle times. The result network speed is faster than nearly all instructions that send results to it[FOOTNOTE].
[FOOTNOTE] The exceptions are taken branch instructions which are faster than the instruction issuer output and register read instructions which are faster than the result network.
When the pipeline is considered as a whole the throughput may be limited either by the rate at which the fetcher can provide FIGs or by the rate at which the functional units consume instructions. The particular instruction mix determines where the limit is imposed. As the typical functional unit cycle time is roughly half of the fetcher's cycle time the throughput of the whole pipeline is limited by the functional units if each FIG contains more than two instructions for any functional unit. If each FIG contains two or fewer instructions for each functional unit then performance will be limited by the fetcher.
It is possibly significant that generally the instruction issuer and the result forwarding network do not limit performance as these are the parts of the system that received the greatest design effort. Instead performance is limited by either the instruction fetcher or the functional units whose design was less involved.
Note that this analysis does not consider the performance effect of data dependencies between instructions or branch instructions which are considered later.
Asynchronous pipeline performance may be degraded by the occurrence of starvation and blocking; that is when individual stages are prevented from operating because the preceding or following stages are not ready to provide or accept data. This problem may be reduced by introducing fifo queues between functional units to decouple them; when one stage performs a slow operation the queue preceding it will fill up, preventing the previous stage from blocking, and the queue following it will empty, preventing the following stage from starving.
SCALP's FIG fifo, instruction queues and result queues perform this decoupling function. [KEAR95] claims that the ideal length for such queues is approximately four times the coefficient of variation of the isolated stage delays. Table 7.10 applies this calculation to the SCALP pipeline. True mean and standard deviation values are dependent on a particular instruction mix; the values used here are rough approximations.
Pipeline Mean Standard Coefficient Ideal Queue
Stage Cycle Time / GD Deviation / GD of Variation Length
FIG Fetch 119 7 0.1 0
Issuer Input 54 2 0.0 0
Issuer Output 31 4 0.1 0
ALU 57 21 0.4 2
Move Unit 60 13 0.2 1
Load / Store 95 20 0.2 1
unit
Register unit 40 3 0.1 0
Result Network 47 25 0.5 2
The length of the queue between two stages should be determined by the greater of the ideal queue lengths in the preceding and following stages. Table 7.11 compares these ideal queue lengths with the queue lengths actually implemented.
Queue Ideal Length Actual Length
FIG queue 0 3
ALU instruction queue 2 2
Move instruction queue 1 2
Load / Store
instruction queue 1 2
Register bank
instruction queue 1 2
ALU result queue 2 1
Move result queue 2 1
Load / Store
result queue 2 1
Register bank
result queue 2 1
These ideal queue lengths must be balanced against other considerations. The large FIG queue helps the instruction issuer to find independent instructions to send to the functional units by considering parts of up to three FIGs simultaneously. On the other hand the shorter than ideal result queues help to reduce the latency of sending results between functional units which is important for code whose performance is limited by data dependencies.
Generally it can be claimed that in view of these results SCALP will not be subject to significant performance degradation resulting from starvation or blocking.
The foregoing results do not consider the effect on performance of taken branches. When a branch is taken the target PC value must be sent to the fetcher and the target instructions processed by the issuer before any further instructions may be executed by the functional units.
The performance of the fetch and issue logic in the presence of branch instructions was measured by connecting the memory, fetcher, instructions fifo, issuer, functional unit instruction queues and branch unit as normal but with no instructions issued to other functional units. The result is given in table 7.12.
Time between taken branches / GD
241
This branch latency is large compared with the cycle times of the functional units: each functional unit could execute four or more instructions in this time. This means that for each taken branch instruction as many as 20 or even more potential instruction execution times are lost. The effect of this on throughput is illustrated in figure 7.4.
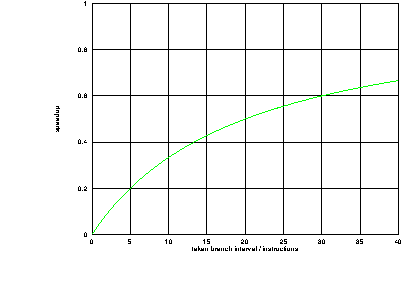
This figure shows that even for very long intervals between taken branches the processor's performance is severely degraded.
There are a number of factors that reduce the significance of this problem:
Some of the execution times after the taken branch may be occupied by independent instructions waiting in other functional units' instruction queues. At most 8 such instructions could be waiting.
Throughput may be limited by data dependencies or by an imbalance in the distribution of instructions among the functional units. In this case the number of potential instructions lost during the branch latency may be lower.
As with any superscalar processor, branch prediction could be added to reduce the effect of the branch latency. The benefit of branch prediction is considered in section 8.3.1.
To validate the results in the previous section and to measure the effect of other factors including data dependencies between instructions the throughput of the processor as a whole was investigated using the examples described in section 7.1.1.
The performance of each of the instruction streams has been measured and the results are shown in table 7.13.
Sequence Time per instruction 5 x Time per instruction
/ GD / GD
dis-ind 29.9 150
ndis-ind 56.5 282
dis-dep 48.1 240
ndis-dep 65.8 329
ind-br 48.3 242
dep-br 87.8 438
As would be expected the greatest performance is achieved by dis-ind, the sequence with instructions evenly distributed among the functional units, few data dependencies and no branches. Performance is reduced when either the distribution is unbalanced, data dependencies are introduced, or branches are taken.
The measure 5 x cycle time can be compared with the cycle times measured in the previous section - the factor of 5 corresponds to the 5 functional units and to the 5 instructions per FIG. This is valid because these sequences contain very few immediate chunks. Only the speed of the best case sequence comes close to being limited by the instruction fetcher. The cycle times of all other sequences are significantly greater than the limits of the fetcher or functional unit throughputs, so they must be limited by unbalanced functional unit use, data dependencies or branch instructions.
ndis-ind is intended to be limited by individual functional unit throughput. Its cycle time of 56.5 GD is close to the typical functional unit cycle times of table 7.7.
dis-dep is intended to be limited by data dependencies between instructions. Its cycle time might be expected to be the sum of the functional unit and result network cycle times (i.e. around 100 GD) yet the measured cycle time is 48.1 GD. This difference can be attributed to the difference between the latency of a block (request in to request out) and the cycle time (request in to next request in); this is clear from pipeline visualisation.
ind-br is intended to be limited by the branch latency and has one taken branch in each five instructions. The cycle time for five instructions closely matches the branch latency measured in table 7.12, indicating that the branch latency is limiting the performance.
The performance of the example programs described in section 7.1.1 has been measured and is shown in table 7.14.
Program Time per instruction
/ GD
qsort 61.7
shading 47.2
strtree 66.2
sumlist 62.9
wc 57.5
Arithmetic mean 58.1
Generally the times measured for these programs are about the same as the times recorded for the instruction sequences with dependences, unbalanced use of the functional units, and branches.
Limits may be imposed on SCALP's performance by a number of different factors depending on the particular code being executed:
The high branch latency means that frequent taken branches substantially reduce performance. This could be alleviated by means of branch prediction.
Concurrency among the functional units can be limited by data dependencies between instructions executing in separate functional units.
Concurrency among the functional units can also be limited by an imbalance in the distribution of instructions between the functional units.
When other factors do not limit performance the cycle time of the FIG fetcher determines the throughput.
The instruction issuer and result network do not generally limit performance.
This section evaluates the parallelism that SCALP is able to achieve between its five functional units. Up to five fold parallelism is possible between the functional units, but how much of this parallelism is actually achieved is dependent on the extent of their utilisation.
Figures 7.5 and 7.6 show the number of functional units active at any time for each of the example instruction sequences and programs.
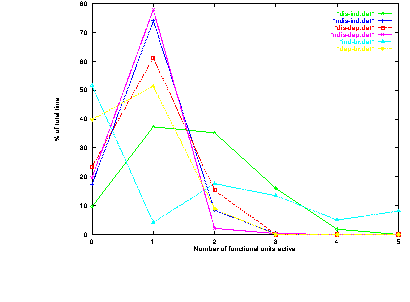
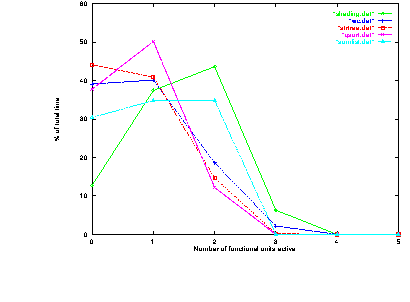
These figures can be interpreted as follows:
When no functional units are active the processor is likely to be experiencing a branch latency. Observe that the instruction sequences with no branches spend relatively little time (less than 25%) with no functional units active; the sequences with branches spend 40-50% of their time thus.
When exactly one functional unit is active the processor is likely to be limited by either data dependencies between instructions or by severe resource contention over one functional unit. The instruction sequences with many data dependencies spend around 50 % to 80 % of the time with one functional unit active; the instruction sequences with severe functional unit contention spend around 75 % to 80 % of the time with one functional unit active. The sequences that have neither contention nor dependencies spend the least time with only one functional unit active.
When more than one functional unit is active the processor is operating free from severe data dependencies or resource contention. Most of the sequences spend less than 15 % of the time with more than one functional unit active. The sequences which are free from resource contention and data dependencies spend around 40 % - 50 % of the time with more than one functional units active.
With these points in mind it can be seen that the example programs spend between around 15 % and 45 % of their time experiencing branch latencies, between around 30 % to 50 % of the time experiencing data dependencies or functional unit contention, and between around 10 % to 50 % of the time free from these impediments.
The programs themselves impose a limit on the amount of functional unit parallelism that is possible. Figure 7.7 shows the amount of time that each functional unit must be active for each example program. From this data it is possible to calculate the maximum possible functional unit parallelism for the programs. This is presented in table 7.15.
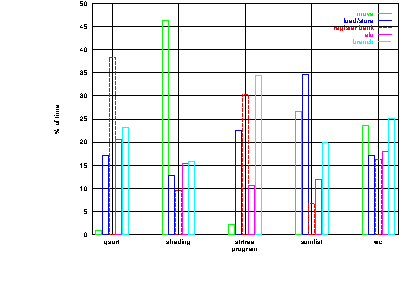
Program Maximum Parallelism
qsort 2.60
shading 2.15
strtree 2.90
sumlist 2.88
wc 3.98
Table 7.16 summarises the average number of functional units actually active for the programs.
The raw values in this table are misleading if compared directly with measures of functional unit parallelism for a synchronous processor. When a synchronous processor's functional unit parallelism is measured it is assumed that the functional units are active for all of the clock cycle; in contrast the asynchronous functional unit is considered inactive as soon as its operation is complete. Table 7.16 also provides a measure which allows for this factor.
Benchmark Functional Unit Parallelism Equivalent Synchronous
Functional Unit Parallelism
dis-ind 1.63 2.34
ndis-ind 0.91 1.24
dis-dep 0.92 1.45
ndis-dep 0.83 1.06
ind-br 1.40 1.45
dep-br 0.69 0.80
shading 1.44 1.48
wc 0.84 1.22
strtree 0.71 1.06
qsort 0.75 1.13
sumlist 1.04 1.11
In comparison [JOHN91] (see appendix A) proposes a number of conventional synchronous superscalar architectures for which the equivalent parallelism measure falls between 1 and 2, typically around one third higher than SCALP.
This section compares the performance of SCALP with the ARM and ARMLESS processors described in section 7.1.1.
Table 7.15 gives the SCALP execution time in gate delays for each of the benchmark programs. Alongside are measurements for ARM and ARMLESS in numbers of cycles.
All ARMLESS instructions take one cycle except taken branches which have a one cycle penalty. For ARM the branch penalty is two cycles; in addition load and store instructions take extra cycles because ARM has a single memory interface.
In order to compare the ARM and ARMLESS results with the SCALP results the cycle times of ARM and ARMLESS have been estimated in terms of gate delays. The values taken are 33 gate delays for ARM and 25 gate delays for ARMLESS. These are approximations based on the clock speeds of ARM and of ARMLESS-like processors and estimates of typical gate delays.
SCALP ARM ARMLESS
GD Cycles GD Cycles GD
Shading 31062 448 14784 384 9600
Word Count 84683 1239 40887 1221 30525
String Tree
Search 15822 222 7326 156 3900
Quicksort 459655 2627 86691 1797 44925
Sumlist 10944 217 7161 136 3400
Geometric Mean 46150 19401 11179
These results show that on average SCALP operates 2.4 times more slowly than ARM and 4.1 times more slowly than ARMLESS.
This result may be attributed to the following factors:
The poor code density reported in section 7.2 means that SCALP must execute more instructions than ARM and ARMLESS.
The cycle times of the individual functional units and other blocks are slower than the cycle times of the synchronous processors. This is considered in section 7.6.
The poor performance results reported in the previous section can be attributed in part to the slowness of the asynchronous control circuits used in parts of the SCALP implementation.
Consider for example the branch unit control circuit described in section 6.6 and shown in figure 6.20. This circuit is typical of the control circuits used in SCALP's functional units. Two points can be observed about this circuit:
The circuit's structure is very much like a flow chart describing the required functionality.
The circuit is very sequential in nature.
In contrast consider how a synchronous implementation of this block would be carried out. Initially a specification could be drawn up describing how each of the control inputs would be considered in turn to decide on the correct action for this cycle. This specification could then be optimised, possibly to as little as three levels of logic, and used as the basis for a finite state machine.
The difference between the synchronous and asynchronous implementations is that there is no optimisation of the asynchronous circuit, resulting in sequential and hence slow behaviour. This is a direct consequence of the macromodule design approach.
An important question at this point is whether optimisation techniques for this type of asynchronous circuit exist, and if so whether they perform as well as well known synchronous (and combinational) optimisation techniques. The answer is that they probably do exist but they are more complex than the synchronous techniques and are less mature. This question is considered further in section 8.3.2.
The combination of a number of factors was intended to increase SCALP's power efficiency. As previous sections have shown in several cases the expected benefits have not been achieved. The following subsections considers the effects of these factors on the processor's overall power efficiency.
Section 7.2 evaluated SCALP's code density in comparison with the ARM and ARMLESS processors and found that it does not achieve any increase. Consequently there will be no increase in power efficiency resulting from decreased processor to memory bandwidth and related activity.
Sections 7.3 and 7.4 considered the parallelism due to pipelining and to the multiple functional units respectively. Section 7.4 concluded that for the example programs the level of parallelism was rarely greater than one. This low level of parallelism was attributed to the effect of
the branch latency;
the presence of data dependencies between instructions;
contention for functional units.
It was also observed that conventional superscalar processors are able to obtain a greater degree of parallelism. Consequently SCALP's power efficiency cannot be better than these conventional architectures in this respect.
One important area in which the SCALP architecture could be improved is the provision of branch prediction which would increase the level of pipeline parallelism. The is considered in section 8.3.1.
The use of asynchronous logic has had two effects on SCALP's power efficiency. Firstly in an asynchronous circuit inactive blocks consume no power; in a conventional synchronous circuit the clock is applied to all blocks at all times. This effect leads to a substantial power saving compared to a synchronous implementation of the SCALP architecure as shown in table 7.18. On the other hand this statistic can be seen as simply reflecting the low utilisation of the available parallelism within the processor.
Program Average % activity of Power Saving
functional units
qsort 14.9 6.7
shading 28.7 3.5
strtree 14.2 7.0
sumlist 20.9 4.8
wc 16.8 6.0
The second effect of the use of asynchronous logic is its influence on the overall speed of the processor. As was observed in section 7.6 the sequential nature of the asyncrhonous control circuits makes them slow in comparison with synchronous circuits. The pipeline stage cycle times shown in table 7.7 are generally greater than the assumed cycles times for ARM and ARMLESS used in section 7.5. To obtain equivalent performance from the synchronous and asynchronous circuits the supply voltages would have to be adjusted, substantially favouring the synchronous circuit.
SCALP's datapath will consume less power when it operates on byte rather than word quantities. The occurance of byte operations in the example programs is not in any sense representative of any real programs and data on the occurance of these operations in real programs is not available, making estimation of the power saving attributable to this factor difficult.
In conclusion SCALP's overall power efficiency is poor in comparison with conventional processors.
Section 7.1.1 described five example programs that have been written for SCALP in order to evaluate its performance. Writing these programs identified problems with the processor's execution model that result in longer code sequences than were expected and hence poor code density - evidenced by the results in section 7.2. This section discusses these problems.
In writing the example programs it became clear that the explicit forwarding mechanism was useful in fewer cases than had been expected. For very many instructions it was necessary to send the result to the register bank, and very many operands were read from registers. Only in relatively few cases could results be sent directly to the functional unit of their next use. Consider the following code which sums the values in an array and saves the sum in another variable in memory:
t = 0
for i in 1 to 1000 loop
t = t + x[i]
end
a = t
Ignoring the loop control and array indexing and concentrating on just the summation, this may be compiled to the following code on a conventional processor:
MOV R2,#0 ; R2 stores variable t
....
L1: LDR R1,[...] ; load x[i] into R1
ADD R2,R2,R1 ; t = t + x[i]
....
BRNE L1 ; do next loop iteration if terminal
; count not reached
STR R2,[...] ; a = t
Consider what happens to the result of the addition in this code. For 999 of the 1000 iterations of the loop the result is written to R2 by the add and read from it in the next iteration by the following add. However in the 1000th iteration it is written to R2 by the add and read by the store corresponding to the assignment to variable a.
If the result of that add was always used by the same destination functional unit (i.e. the ALU) then the add could be encoded as follows:
add -> alu_a
but in this case there are two possible destinations. The only general solution is to use the register bank:
add -> regd
write 2
and to read from the register bank when the destination is known. In this case there are ways of avoiding the problem, such as the following:
for i in 1 to 1000 loop
t = t + x[i]
end
a = t + 0
for i in 1 to 999 loop
t = t + x[i]
end
t = t + x[1000]
a = t
In the first of these examples an additional "dummy" addition is carried out so that the result of the add within the loop is always sent to the same destination, the ALU. In the second example the last iteration of the loop is unrolled so that the result of the last addition can be sent to a different destination. However these two "tricks" cannot be applied in other more general cases, and in the example programs it was often found necessary to write results to temporary registers.
Of all the example programs the most inefficient in terms of explicit forwarding was the quicksort program. Because of the nature of the program virtually all branches are highly data-dependent. Its typical behaviour is to load a value from memory and compare it with some other value. Whether the value will be used again and if so where it will be used is not known until the result of the comparison has been computed.
An important observation about these examples is that they are consistent with the data in table 5.1 but they indicate that that data is slightly misleading. It is true to say that in a dynamic instruction trace 64 % of instruction results are used exactly once, but it is not true to say that for 64 % of static instructions the result is always used by exactly one subsequent instruction. As far as code generation for SCALP is concerned it is this static property that is important.
Section 8.2 returns to this problem to consider ways in which the architecture can be improved.
Next Chapter






